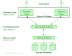
QUICK SORT

Quick Sort is a divide and conquer algorithm. It first divides a large array into two smaller sub-arrays: the low elements and the high elements. Then, It recursively sort the sub-arrays.
The steps are:

• Pick an element, called a pivot, from the array.
• Partitioning: reorder the array so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation.
• Recursively apply the above steps to the sub-arrays of elements separately.

The base case of the recursion is arrays of size zero or one, which never need to be sorted.
The pivot selection and partitioning steps can be done in several different ways; the choice of specific implementation schemes greatly affects the algorithm's performance.

The different ways of pivot selection are:

1. Always pick first element as pivot.
2. Always pick last element as pivot (implemented below)
3. Pick a random element as pivot.
4. Pick median as pivot.

EXAMPLE

QUICK SORT C-CODE

// C program for implementation of Quick sort
#include <stdio.h>
// A utility function to swap two elements
void swap(int* x, int* y)
{
    int t = *x;
    *x = *y;
    *y = t;
}

/* This function takes last element as pivot, places the pivot element at its correct position in sorted array, and places all smaller (smaller than pivot) to left of pivot and all greater elements to right of pivot */
int partition(int arr[], int low, int high)
{
    int temp;
    int pivot = arr[high];    // pivot
    int i = (low - 1);  // Index of smaller element

    for (int j = low; j <= high- 1; j++)
    {
        // If current element is smaller than or equal to pivot
        if (arr[j] <= pivot)
        {
            i++;    // increment index of smaller element
            swap(&arr[i], &arr[j]);
        }
    }
    swap(&arr[i + 1], &arr[high]);
    return (i + 1);
}

/* The main function that implements QuickSort
 arr[] --> Array to be sorted,
  low  --> Starting index,
  high  --> Ending index */
void quickSort (int arr[], int low, int high)
{
    if (low < high)
    {
        // pi is partitioning index, arr[p] is now at right place 
        int pi = partition(arr, low, high);

        // Separately sort elements before and after partition
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}
 int main()
{
    int arr[] = {6, 3, 5, 2, 8, 10, 9};
    int n = sizeof(arr)/sizeof(arr[0]);
    int i, j,temp;
    //Quick Sort calling
    quickSort(arr, 0, n-1);
    printf("Sorted array: \n");
    for (int i=0; i < n; i++)
    {
        printf("%d ", arr[i]);
    }
    return 0;
}

Output

Sorted array:
2  3  5  6  8  9  10

COMPLEXITY ANALYSIS

• Best and Average Case Time Complexity: O(nLog(n) ).
• Worst Case Time Complexity: O(n*n).
• Auxiliary Space Complexty: O(n).