MERGE SORT

Unknown 15:38
Merge Sort is a divide and conquer algorithm that was invented by John von Neumann in 1945.
Conceptually, a merge sort works as follows:
  • Divide the unsorted list into n sublists, each containing 1 element (a list of 1 element is considered sorted).
  • Repeatedly merge sublists to produce new sorted sublists until there is only 1 sublist remaining. This will be the sorted list.
    It a stable sort, which means that the implementation preserves the input order of equal elements in the sorted output.

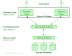
    EXAMPLE

    Reference: Wikipedia

    MERGE SORT C-CODE


    // C program for implementation of Merge sort
#include <stdio.h>
// Merges two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge(int arr[], int l, int m, int r)
{
    int i, j, k;
    int n1 = m - l + 1;
    int n2 =  r - m;

    /* create temp arrays */
    int L[n1], R[n2];

    /* Copy data to temp arrays L[] and R[] */
    for (i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for (j = 0; j < n2; j++)
        R[j] = arr[m + 1+ j];

    /* Merge the temp arrays back into arr[l..r]*/
    i = 0; // Initial index of first subarray
    j = 0; // Initial index of second subarray
    k = l; // Initial index of merged subarray
    while (i < n1 && j < n2)
    {
        if (L[i] <= R[j])
        {
            arr[k] = L[i];
            i++;
        }
        else
        {
            arr[k] = R[j];
            j++;
        }
        k++;
    }
    // Copy the remaining elements of L[], if there are any
    while (i < n1)
    {
        arr[k] = L[i];
        i++;
        k++;
    }
    // Copy the remaining elements of R[], if there are any
    while (j < n2)
    {
        arr[k] = R[j];
        j++;
        k++;
    }
}
/* l is for lower index and u is upper index of the
   sub-array of arr to be sorted */
void mergeSort(int arr[], int l, int u)
{
    if (l < u)
    {
        // Same as (l+u)/2, but avoids overflow for
        // large l and h
        int m = l+(u-l)/2;
        // Sort first and second halves
        mergeSort(arr, l, m);
        mergeSort(arr, m+1, u);
        merge(arr, l, m, u);
    }
}
 int main()
{
    int arr[] = {6, 3, 5, 2, 8, 10, 9};
    int n = sizeof(arr)/sizeof(arr[0]);
    int i, j,temp;
    //Merge Sort calling
    mergeSort(arr, 0, n - 1);
    printf("Sorted array: \n");
    for (int i=0; i < n; i++)
    {
        printf("%d ", arr[i]);
    }
    return 0;
}

    OutputSorted array:
    2  3  5  6  8  9  10

    COMPLEXITY ANALYSIS

    • Best, Average and Worst Case Time Complexity: O(nLog(n) ).
    • Auxiliary Space Complexity: O(n).

    Tags: